设椭圆方程为x2/a2+y2/b2=1,两边对x取导数得:2x/a2+2yy'/b2=0,故椭圆上任意一点(x,y)处的切线的斜率k=y'=-b2x/(a2y);若M(x0,y0)是椭圆上的任意一点,那么过M的切线方程为:y=[-b2x0/(a2y0)](x-x0)+y0。
椭圆切线方程公式的推导过程

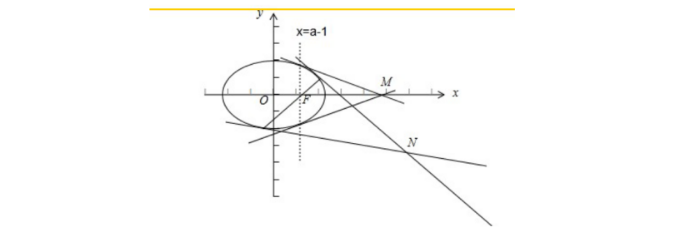
直线与椭圆的位置关系
直线与椭圆的位置关系有三种,相离,相切,相交。
1.直线与椭圆相离的充要条件是直线与椭圆的方程所组成的方程组无解,即转化为所得的,一元二次方程的根的判别式小于0。
2.直线与椭圆相切的充要条件是直线与椭圆的方程所组成的方程组有唯一解,即转化所得的,一元二次方程的根的判别式等于0。
3.直线与椭圆相交的充要条件是直线与椭圆的方程所组成的方程组有两个不相同的解,即转化为所得的一元二次方程的根的判别式大于0。