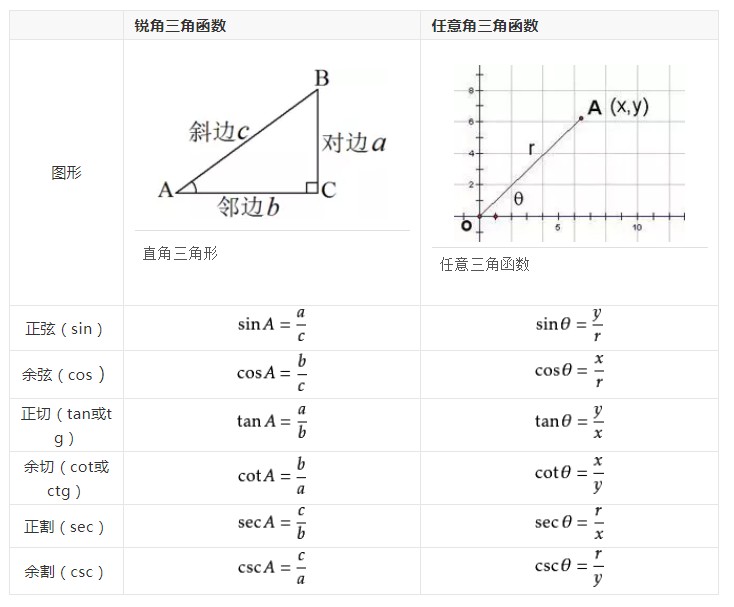
常见的三角函数包括正弦函数、余弦函数和正切函数。三角函数一般用于计算三角形中未知长度的边和未知的角度,下面就和小编整理的常用三角函数公式,供大家参考。
常用三角函数公式整理
积化和差公式
sinα·cosβ=(1/2)*[sin(α+β)+sin(α-β)]
cosα·sinβ=(1/2)*[sin(α+β)-sin(α-β)]
cosα·cosβ=(1/2)*[cos(α+β)+cos(α-β)]
sinα·sinβ=-(1/2)*[cos(α+β)-cos(α-β)]
和差化积公式
sinα+sinβ=2sin[(α+β)/2]·cos[(α-β)/2]
sinα-sinβ=2cos[(α+β)/2]·sin[(α-β)/2]
cosα+cosβ=2cos[(α+β)/2]·cos[(α-β)/2]
cosα-cosβ=-2sin[(α+β)/2]·sin[(α-β)/2]
三倍角公式
sin3α=3sinα-4sin^3α;
cos3α=4cos^3α-3cosα
两角和与差的三角函数关系
sin(α+β)=sinαcosβ+cosαsinβ
sin(α-β)=sinαcosβ-cosαsinβ
cos(α+β)=cosαcosβ-sinαsinβ
cos(α-β)=cosαcosβ+sinαsinβ
tan(α+β)=(tanα+tanβ)/(1-tanα·tanβ)
tan(α-β)=(tanα-tanβ)/(1+tanα·tanβ)
正弦二倍角公式
sin2α=2cosαsinα
推导:sin2A=sin(A+A)=sinAcosA+cosAsinA=2sinAcosA
拓展公式:sin2A=2sinAcosA=2tanAcos2A=2tanA/[1+tan2A]
1+sin2A=(sinA+cosA)^2
余弦二倍角公式
余弦二倍角公式有三组表示形式,三组形式等价:
1.Cos2a=Cos2a-Sin2a=[1-tan2a]/[1+tan2a]
2.Cos2a=1-2Sin2a
3.Cos2a=2Cos2a-1
推导:cos2A=cos(A+A)=cosAcosA-sinAsinA=cos^2A-sin^2A=2cos^2A-1
=1-2sin^2A
正切二倍角公式
tan2α=2tanα/[1-tan2α]
推导:tan2A=tan(A+A)=(tanA+tanA)/(1-tanAtanA)=2tanA/[1-tan2A]
降幂公式
cosA^2=[1+cos2A]/2
sinA^2=[1-cos2A]/2
tanA^2=[1-cos2A]/[1+cos2A]
变式:
sin2α=sin^2(α+π/4)-cos^2(α+π/4)=2sin^2(a+π/4)-1=1-2cos^2(α+π/4);cos2α=2sin(α+π/4)cos(α+π/4)
余弦定理:
a^2=b^2+c^2-2bc*cosA
b^2=c^2+a^2-2ca*cosB
c^2=a^2+b^2-2ab*cosC
三角函数的定义式