在同一个二维平面内,由两组平行线段组成的闭合图形称为平行四边形。根据平行四边形的性质:如果一个四边形是平行四边形,那么这个四边形的两条对角线互相平分。所以平行四边形对角线互相平分是正确的。
平行四边形一般用图形名称加四个顶点依次命名。注:在用字母表示四边形时,一定要按顺时针或逆时针方向注明各顶点。
平行四边形对角线互相平分证明方法:
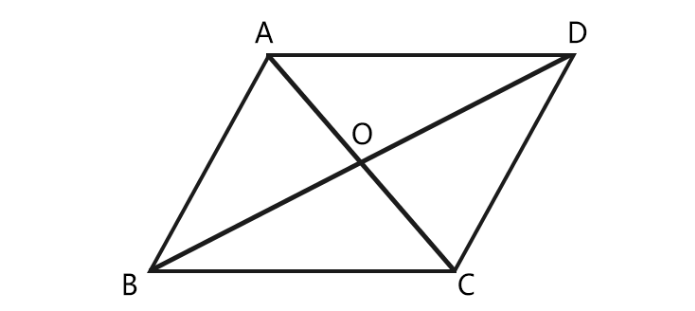
设平行四边形ABCD的对角线AC、BD交于O 求证OA=OCOB=OD
证明:
∵四边形ABCD是平行四边形,
∴AB//CDAD//BC
∴∠ABD=∠CDB∠ADB=∠CBD
又∵AC=CA
∴△ABD≌△CDB(ASA)
∴AB=CD
又∵∠ABD =∠CDB∠AOB=∠COD
∴△AOB≌△COD(AAS)
∴OA=OCOB=OD